Phylogenetic Trees
Just as a geneologist might construct a family tree to illustrate ancestors and descendents within a human family, systematic biologists (taxonomists) construct phylogenetic trees to depict relationships among groups of living organisms. There are several ways to create such trees. The method chosen often depends on the distinctiveness of each taxon, the type and quality of categorical data available, and the scientist’s overall philosophy toward classification.
Proponents of evolutionary systematics attempt to produce a phylogenetic tree (dendrogram) that faithfully reproduces a taxon’s lineage: each junction point represents a common ancestry and the length of each branch reflects the amount (or duration) of evolutionary divergence from the presumed ancestor. Even under the best of circumstances, developing such a dendrogram requires a great deal of speculation because the fossil record is often fragmentary (or entirely absent).
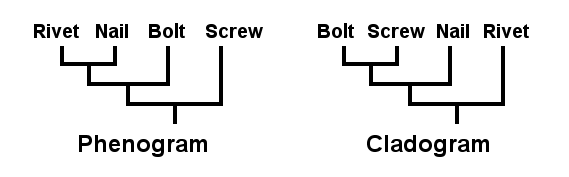
Some systematic biologists argue that it is pointless to create an evolutionary tree because there is no way to prove whether it is right or wrong. Instead, they advocate the phenetic approach to classification: grouping organisms entirely on the basis of physical similarities. In a phenogram, each branch point represents a step of increasing similarity – taxa which share the most characters (both primitive and advanced) perch next to one another in the family tree even though they do not necessarily share a common ancestor.
There is another approach, cladistics, that is gaining adherents because it strives to reflect evolutionary lineage without “creating” hypothetical ancestors. This is accomplished by first using an “outgroup” to determine which characteristics are “primitive” (ancestral) and which are “advanced” (derived). A cladogram is constructed by grouping taxa that share the greatest number of derived characters. Adjacent taxa are called “sister groups” or “clades”. They are usually presumed to be descendents of a common ancestor.
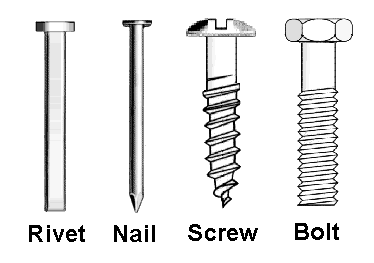
Dr. Lewis L. Deitz, a systematic entomologist at North Carolina State University, has cleverly illustrated the distinction between cladistic and phenetic analyses by imagining the evolution of metal “fasteners” including the “rivet”, the “nail”, the “screw” and the “bolt”. According to Dr. Deitz, the “rivet” has the simplest structure and, therefore, he presumes it to be the common ancestor of all fasteners. Among the other fasteners, there are at least seven derived character states (physical characteristics not found in “rivets”: 1.) notched heads, 2.) rounded heads, 3.) hex heads, 4.) threaded shafts, 5.) tapered shafts, 6.) pointed tips, and 7.) thick diameter.
The character states of all four fasteners are compared in the following table where the symbol “0” represents the pleisiomorphic (primitive or “rivet-like”) state and “1” represents the apomorphic (derived or evolved) state.